公开密钥加密

概述

参考：

• Wiki, PKC 英文
• Wiki, 数字签名
• 阮一峰
• 知乎,RSA 的公钥和私钥到底那个才是用来加密和哪个用来解密
• Wiki, 公开密钥加密 中文
• https://arthurchiao.art/blog/everything-about-pki-zh

• 甲方选择某种加密规则，对信息进行加密
• 乙方使用同一种规则，对信息进行解密

由于加密和解密使用同样规则（简称"密钥"），这被称为 Symmetric-key algorithm(对称密钥算法)。这种加密模式有一个最大弱点：甲方必须把加密规则告诉乙方，否则无法解密。保存和传递密钥，就成了最头疼的问题。因为大多数情况下，其实两方之间的通信，只有一方是需要加密的，另一方只需要知道信息内容。

1976 年，两位美国计算机学家 Whitfield Diffie 和 Martin Hellman，提出了一种崭新构思，可以在不直接传递密钥的情况下，完成解密。这被称为"Diffie-Hellman 密钥交换算法"。这个算法启发了其他科学家。人们认识到，加密和解密可以使用不同的规则，只要这两种规则之间存在某种对应关系即可，这样就避免了直接传递密钥。

这种新的加密模式就被称为"非对称密钥算法"。

（1）乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的。 （2）甲方获取乙方的公钥，然后用它对信息加密。 （3）乙方得到加密后的信息，用私钥解密。

如果公钥加密的信息只有私钥解得开，那么只要私钥不泄漏，通信就是安全的。

1977 年，三位数学家 Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做 RSA 算法。从那时直到现在，RSA 算法一直是最广为使用的"非对称加密算法"。毫不夸张地说，只要有计算机网络的地方，就有 RSA 算法。

这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长 RSA 密钥是 768 个二进制位。也就是说，长度超过 768 位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024 位的 RSA 密钥基本安全，2048 位的密钥极其安全。

PKC 特点

• 这种加密方式，需要一对密钥。只有公钥可以加密，私钥不能用来加密数据。
• Public key(公钥) # 公开给所有人。用来加密数据、验证签名。使用公钥把明文加密后所得的密文，只能使用对应的私钥才能解密并得到原本的密文。反之不行。
• Secret key(私钥) # 自己留存，必须保证其私密性。用来解密数据、签名。使用私钥创建数字签名，只能使用公钥才能验证该数字签名的有效性。反之不行。
  • 一般情况，密钥对是通过程序自动生成的。首先生成私钥后，公钥包含在私钥当中
• Digital signature(数字签名)。签名提供的是真实性，而不是保密性。
  • 所谓的数字签名，就像人们日常生活中在文件上签字一样，都是签名的一种。
  • 而所谓的验证签名，其实就像日常生活中，看看签名的人的笔记与签名是否一致，等等类似的行为

总结一下：既然是加密，那肯定是不希望别人知道发送给我的消息，所以只有我才能解密，所以可得出公钥负责加密，私钥负责解密；同理，既然是签名，那肯定是不希望有人冒充我发消息，只有我才能发布这个签名，所以可得出私钥负责签名，公钥负责验证。

• 这种加密方式由于是单向加密、单向解密，所以如果双方都想要加密，则需要两对密钥，双方各自用对方的公钥加密信息发送给对方，然后双方再用自己的私钥解密阅读信息。

Signature(签名)

Signature(签名) 的前身是 Message Authentication Code(消息认证码，简称 MAC)，都是用来验证某个 Entity(实体) 发送的消息没有被篡改。

MAC 的原理：

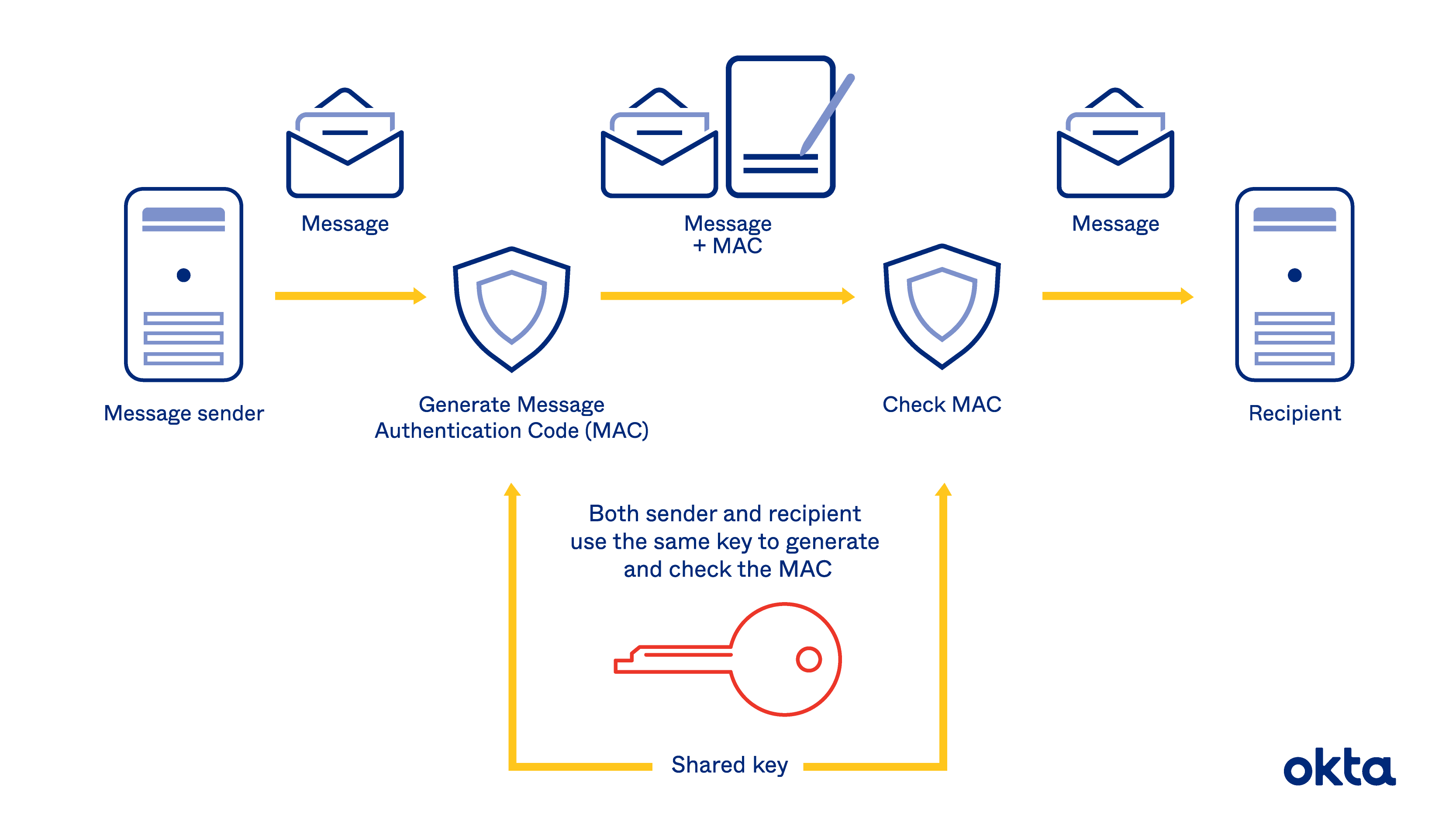
• 对 message(消息) 和 shared secret，a password(双方都知道的一个密码) 做哈希，得到的哈希值就是 MAC；
• 发送方将消息连带 MAC 一起发给接收方；
• 接收方收到消息之后，用同一个密码来计算 MAC，然后跟消息中提供的 MAC 对比。如果相同，就证明未被篡改。

关于哈希：

• 哈希是单向的，因此无法从输出反推输入。这一点至关重要：否则截获消息的人就可以根据 MAC 和哈希函数反推出你的 secrets。
• 此外，生成 MAC 的哈希算法选择也至关重要，本文不会展开，但 提醒一点：不要试图用自己设计的 MAC 算法。
• 最常用的 MAC 算法是 HMAC（hash-based message authentication code）。

但是 MAC 的缺点是：

• 至少有两个 Entity 需要知道共享的密码，所以双方都可以生成 MAC，因此给定一个合法的 MAC，我们无法知道是谁生成的

为了解决这个问题，我们可以通过 PKC，使用私钥签名、公钥验签的方式避免 MAC 的缺点，这，就是 PKC 的 Signature(签名) 功能。正因为对一个已经签名消息只能使用公钥验证，且只能使用对应的私钥生成。因此对于接收方来说，它只能验证签名是否合法，而无法生成同样的签名。

如果只有一个 Entity 知道密钥，那么这种特性就称为 non-repudiation(不可否认性)，即持有私钥的人无法否认数据是由他签名的这一事实。

总结

MAC 与 signature 都叫做签名，是因为它们和现实世界中的签名是很像的。例如，如果想让某人同意某事，并且事后还能证明他们当时的确同意了，就把问题写下来，然后让他们 手写签字（签名）。

通常人们常说的 Digital signature(数字签名)，其实就是基于 PKC 的公钥与私钥这种非对称特点而实现的签名行为。只不过是数字的签名，该签名是存在与计算机世界中的数字形态~~~

总结

公钥加密是数学给计算机科学的神秘礼物， 其数学基础 显然很复杂，但如果只是使用，那并不理解它的每一步数学原理。 公钥加密使计算机能做一些之前无法做的事情：它们现在能看到对方是谁了。 这句话的意思是说，公钥加密使一台计算（或代码）能向其他计算机或程序证明， 不用直接分享某些信息，它也能知道该信息。更具体来说，

• 以前要证明你有密码，就必须向别人展示这个密码。但展示之后，任何有这个密码的人就都能使用它了。
• 私钥却与此不同。你能通过私钥对我的身份进行认证（authenticate my identity），但却无法假冒我。例如，你发给我一个大随机数，我对这个随机数进行签名，然后将再发送给你。 你能用公钥对这个签名进行认证，确认这个签名（消息）确实来自我。 这就是一种证明你在和我（而不是别的其他的人）通信的很好证据。这使得网络上的 计算机能有效地知道它们在和谁通信。这听起来是一件如此理所当然的事情，但仔细地想一下，网络上只有流动的 0 和 1， 你怎么知道消息来自谁，在和谁通信？因此公钥加密系统是一个非常伟大的发明。

应用场景 与 缺点

• 如果 A 持有私钥，B 持有对应公钥。那么此时 B 用对方的公钥加密一个对称密钥并发送给 A，A 使用私钥解密，以获得 B 发送的对称密钥，这时再发送的数据可以使用对称加密。
• 在互联网的 C/S 架构场景中。Server 公开公钥，Client 使用公钥加密信息发送给 Server(发送密码等敏感信息)，Server 使用私钥解密后响应时，使用私钥签名，以便 Client 可以用公钥验证 Server 的真实性(防止钓鱼网站)。
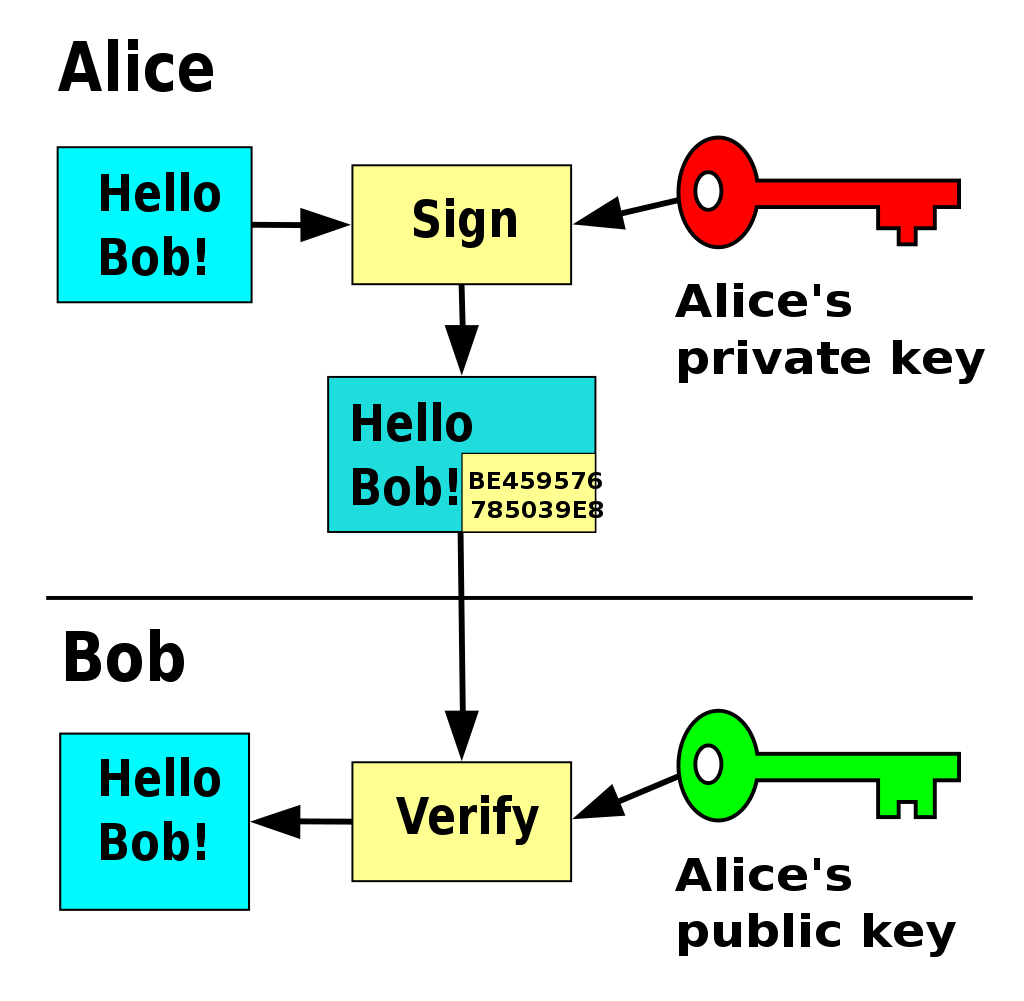
• 如图所示，Alice 在一条消息的末尾签了名，消息内容是 Hello Bob!，这段签署的内容一般是对消息内容进行 hash 计算后，使用 Alice 的私钥的出来的。鲍勃同时收到消息和签名。他使用 Alice 的公钥来验证消息的真实性，即，如果使用公钥计算得出来的消息与原始消息完全匹配，那就证明，这条消息确实是 Alice 发送的。

算法：

• RSA
• DSA
• ELGamal

缺点

公钥加密可能出现的问题：当两者需要通信的时候，需要把公钥发送给对方，但是公钥是谁都可以获取的，那么在二者通信过程中，公钥就有可能被劫持，当公钥被劫持，劫持者把自己的公钥再发送给对方，那么双发再收到的信息，就是被劫持者篡改过的信息了。

• 证书 与 PKI 可以解决以上问题